Parallel Implementation

In an ab-initio approach, the system is driven by electrostatic interactions between the nuclei and electrons. Calculating the electrostatic energy involves computing several terms: (1) quantum mechanical kinetic energy of non-interacting electrons, (2) Coulomb interaction between electrons or the Hartree energy, (3) correction of the Hartree energy to account for the quantum nature of the electrons or the exchange-correlation energy, and (4) interaction of electrons with atoms in the system or the external energy. Hence, CPAIMD computations involve a large number of phases (Figure 1) with high interprocessor communication. These phases are discretized into a large number of virtual processors which generate a lot of communication, but ensures efficient interleaving of work. The various phases are:

Figure 1: Flow of control in OPENATOM

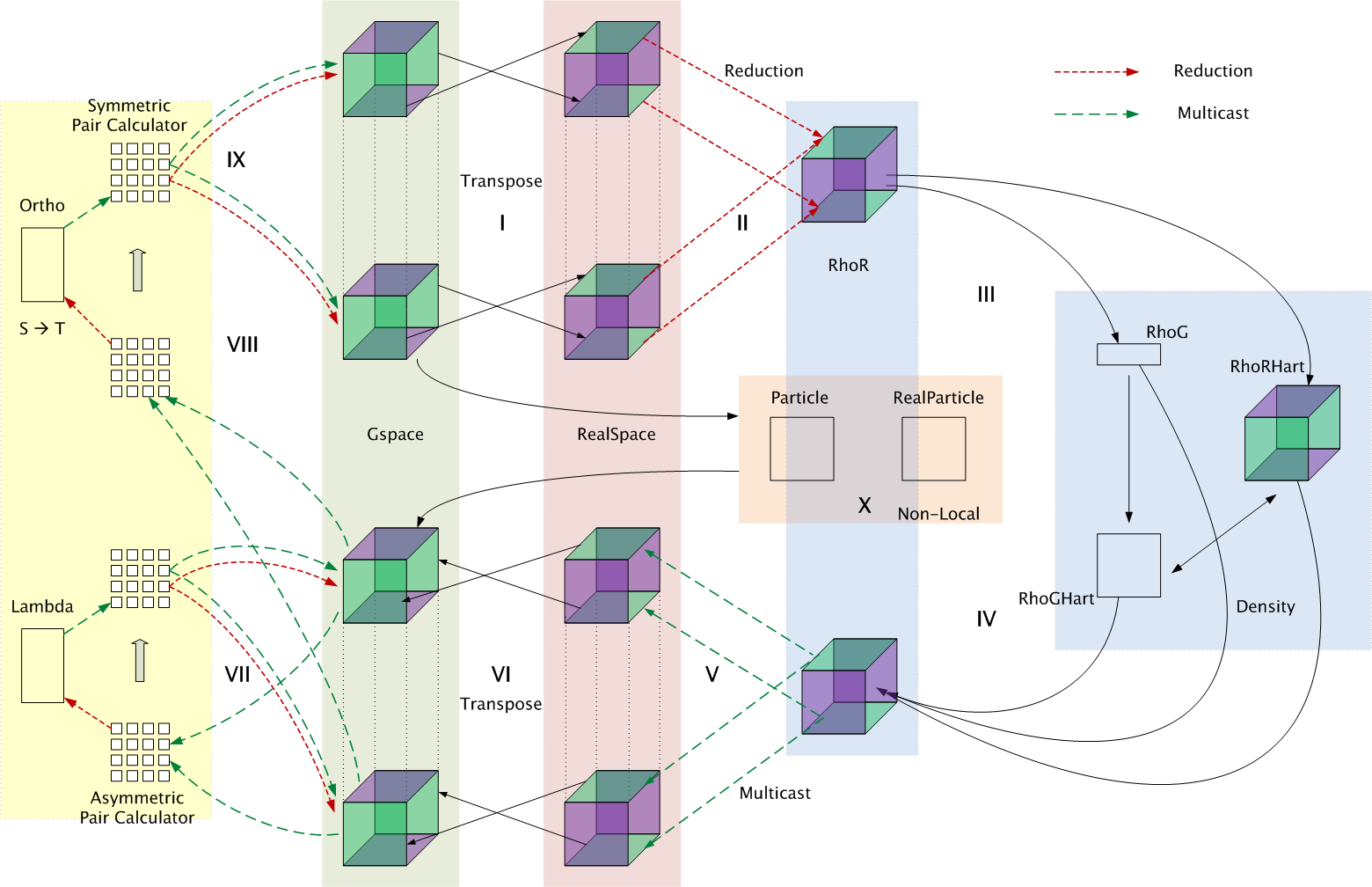• Phase I: In this phase, the real-space representation of the electronic states is obtained from the g-space representation through a transpose based 3-dimensional Fast Fourier Transform (FFT).

• Phase II: Electron density in real-space is obtained via reductions from the real-space state representation.

• Phase III: Fourier components of the density in g-space are created from the corresponding copy in real-space through a 3D FFT.

• Phase IV: Once we have the g-space copy, it is used to compute the ``Hartree and external energies" via multiple 3D FFTs which can be performed independently.

• Phase V: The energies computed in the previous phase are reduced across all processors and send to the corresponding planes of the different states through multicasts. This is exactly reverse of the procedure used to obtain the density in phase II.

• Phase VI: In this phase, the forces are obtained in g-space from real-space via a 3D FFT.

• Phase VII: For functional minimization, force regularization is done in this phase by computing the overlap matrix Lambda (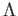$\Lambda$) and applying it. This involves several multicasts and reductions.

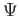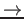• Phase VIII: This phase is similar to Phase VII and involves computation of the overlap matrix Psi ($\Psi$) and its inverse square root (referred to as the S $\rightarrow$ T process) to obtain ``reorthogonalized" states. This phase is called orthonormalization.

• Phase IX: The inverse square matrix from the previous phase is used in a ``backward path" to compute the necessary modification to the input data. This again involves multicasts and reductions to obtain the input for phase I of the next iteration.

• Phase X: Since Phase V is a bottleneck, this phase is interleaved with it to perform the non-local energy computation. It involves computation of the kinetic energy of the electrons and computation of the non-local interaction between electrons and the atoms using the EES method [7].

For a detailed description of this algorithm please refer to [6]. We will now proceed to understand the communication involved in these phases through a description of the various chare arrays involved and dependencies among them.