The ten phases described in the previous section are parallelized by
decomposing the physical system into 15 chare arrays of different dimensions
(ranging between one and four). A description of these objects and communication
between them follows:
- GSpace and RealSpace: These represent the g-space and real-space
representations of the electronic states. They are 2-dimensional arrays
with states in one dimension and planes in the other. They are represented by
![$G(s, p) [n_s \times N_g]$](img5.png) and
and
![$R(s, p) [n_s \times N]$](img6.png) respectively. GSpace
and RealSpace interact through transpose operations in Phase I and hence all
planes of one state of GSpace interact with all planes of the same state of
RealSpace. RealSpace also interacts with RhoR through reductions in Phase II.
respectively. GSpace
and RealSpace interact through transpose operations in Phase I and hence all
planes of one state of GSpace interact with all planes of the same state of
RealSpace. RealSpace also interacts with RhoR through reductions in Phase II.
- RhoG and RhoR: They are the g-space and real-space representations of
electron density and are 1-dimensional (1D) and 2-dimensional (2D) arrays
respectively. They are represented as
![$G_{\rho}(p) [N_{g \rho}]$](img7.png) and
and
![$R_{\rho}(p, p') [(N / N_y) \times N_y]$](img8.png) . RhoG is obtained from RhoR in Phase
III through two transposes.
. RhoG is obtained from RhoR in Phase
III through two transposes.
- RhoGHart and RhoRHart: RhoR and RhoG are used to compute their
Hartree and exchange energy counterparts through several 3D FFTs (in Phase IV).
This involves transposes and point-to-point communication. RhoGHart and RhoRHart
are 2D and 3D arrays represented by
![$G_{HE}(p, a) [N_{gHE} \times
n_{atom-type}]$](img9.png) and
and 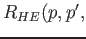
![$a) [(1.4N / N_y) \times N_y \times
n_{atom-type}]$](img11.png) .
.
- Particle and RealParticle: These two 2D arrays are the g-space and
real-space representations of the non-local work and denoted as
![$G_{nl}(s, p)\
[n_s \times N_g]$](img12.png) and
and
![$R_{nl}(s, p) [n_s \times 0.7N]$](img13.png) . Phase X for the
non-local computation can be overlapped with Phases II-VI and involves
communication for two 3D FFTs.
. Phase X for the
non-local computation can be overlapped with Phases II-VI and involves
communication for two 3D FFTs.
- Ortho and CLA_Matrix: The 2D ortho array,
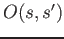 does the
post-processing of the overlap matrices to obtain the T-matrix from the
S-matrix. There are three 2D CLA_Matrix instances used in each of the steps of
the inverse square method (for matrix multiplications) used during
orthonormalization. In the process, these arrays
communicate with the paircalculator chare arrays mentioned next.
does the
post-processing of the overlap matrices to obtain the T-matrix from the
S-matrix. There are three 2D CLA_Matrix instances used in each of the steps of
the inverse square method (for matrix multiplications) used during
orthonormalization. In the process, these arrays
communicate with the paircalculator chare arrays mentioned next.
- PairCalculators: These 4-dimensional (4D) arrays are used in the
force regularization and orthonormalization phases (VII and VIII). They
communicate with the GSpace, CLA_Matrix and Ortho arrays through multicasts and
reductions. They are represented as
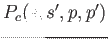 of dimensions
of dimensions
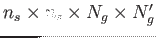 . A particular state of the GSpace array
interacts with all elements of the paircalculator array which have this state in
one of its first two dimensions.
. A particular state of the GSpace array
interacts with all elements of the paircalculator array which have this state in
one of its first two dimensions.
- Structure Factor: This is a 3D array used when we do not use the
EES method for the non-local computation.
Nikhil Jain
2015-08-14