PairCalculator computes the electron state pairwise psi and force updates for CP_State_GSpacePlane. More...
Namespaces | |
| cp | |
| Class for paircalc config data. | |
Classes | |
| class | PairCalculator |
Functions | |
| CkReductionMsg * | sumMatrixDouble (int nMsg, CkReductionMsg **msgs) |
| forward declaration More... | |
| CkReductionMsg * | sumBlockGrain (int nMsg, CkReductionMsg **msgs) |
| void | manmult (int numrowsA, int numRowsB, int rowLength, double *A, double *B, double *C, double alpha) |
Detailed Description
PairCalculator computes the electron state pairwise psi and force updates for CP_State_GSpacePlane.
It can be directed to enact orthonormalization constraints on Psi via Ortho, which are then applied to the input states and returned to CP_State_GSpacePlane. In the dynamics case it performs additional functions based on additional inputs.
Paircalculator (and ortho) are used to satisfy the orthogonality constraint. 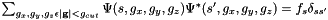
PairCalculator (PC) is a 4D chare array that is, at its heart, a glorified wrapper for a bunch of matrix multiplications. It serves the function of managing the complexity of the decomposition and communication logic that is required to scale well. In the process, it introduces some more :).
There are two separate PairCalc chare arrays instantiated per OpenAtom simulation instance. Both of these serve GSpace and process data whenever invoked by GSpace. Both these PC arrays share a single Ortho chare array to which some of the multiply work is delegated.
The extra complications are for parallelization and the multiplication of the forces and energies.
In normal use the calculator is created. Then forces are sent to it and multiplied in a big dgemm. Then this result is reduced to the answer matrix and shipped back. The received left and/or right data is retained for the backward pass which is triggered by the finishPairCalc call. This carries in another set of matrices for multiplication. The results are again reduced and cast back. Thus terminating the life cycle of the data in the pair calculator. As the calculator will be reused again throughout each iteration the calculators themselves are only created once.
The paircalculator is a 4 dimensional array. Those dimensions are: w: gspace state plane (the second index of the 2D gspace) x: coordinate offset within plane (a factor of grainsize) y: coordinate offset within plane (a factor of grainsize) z: chunk offset within array of nonzero points So, for an example grainsize of 64 for a 128x128 problem:
* numStates/grainsize gives us a 2x2 decomposition.
* 1st quadrant ranges from [0,0] to [63,63] index [w,0,0,0]
* 2nd quadrant ranges from [0,64] to [63,127] index [w,0,64,0]
* 3rd quadrant ranges from [64,0] to [127,63] index [w,64,0,0]
* 4th quadrant ranges from [64,64] to [127,127] index [w,64,64,0]
0 64 127
0 _________
| | |
| 1 | 2 |
64 ---------
| | |
| 3 | 4 |
127 ---------
Further complication arises from the fact that each plane is a cross-section of a sphere. So the actual data is sparse and is represented by a contiguous set of the nonzero elements. This is commonly referred to as numPoints or size within the calculator.
In the dynamics case there are two additional complications. In the backward path of the asymmetric pairCalculator we will receive 2 input matrices, gamma and orthoT. Where orthoT came from the orthonormalization following the symmetric pairCalculator. And gamma was produced by a multiplication with orthoT in the Ortho object.
If ortho falls out of tolerance then Ortho will signal the GSP that a tolerance update is needed. We then proceed with the psi calculation as normal. On receipt of newpsi, Gspace will then react by sending the PC the Psi velocities (PsiV) in the same way (acceptLeft/RightData) that it sends Psi, but with the psiv flag set true. These will be recorded in the left data array. We will then multiply with the orthoT we kept from the previous invocation (psi) of the backward path. We then ship the corrected velocities back to gspace via the acceptnewVpsi reduction. Same procedure as for acceptnewpsi, just a different entry method.
Fourth dimension decomposition is along the axis of the nonzero values in gspace. Therefore it is fundamentally different from the 2nd and 3rd dimensions which divide the states up into (states/grainsize)^2 pieces. The fourth dimension divides along the nonzeros of gspace. A X,0,0,N division will have the entirety of a state, but only a K/Nth (where K is the number of nonzero elements) chunk of the nonzero values. It can therefore perform the dgemm on that chunk, its multicast degree will be 1, and have a portion of the total solution. Thereby reducing the PC inbound communication volume substantially. This comes at the cost of an additional reduction. The result for the nonzero chunks has to be pasted together to form the result for the entire nonzero. Then the results are summed together across the planes to produce the complete S or L matrix. Only the first of those reductions is new.
More about this "extra" reduction. If we consider the Multiply as C = AB. Where A is nstates x numpoints and B is numpoints x nstates to result in C of nstates x nstates. The 4th dim decomposition chops only the inner index numpoints. Thereby resulting in numblocks C submatrices all of size nstates x nstates. Making C from numblock C(i) is just matrix addition. So for the forward path there is in fact no "extra" reduction or stitching necessary for the 4th dim decomposition. All the "stitching" is in the statewise decompostion for the forward path. So the only change for the forward path is in adding the numblock elements to the reduction tree.
An important distinction between these methods is that in the absence of a grainsize decomposition the sections for the second reduction to ortho are essentially arbitrary with respect to the PairCalculator decomposition.
Similarly, the backward path for a chunk with grainsize==nstates needs input matrices of size nstates X nstates. Which means that the backward path cannot proceed until all ortho sections broadcast their pieces of the input matrices. The backward path reduction to gspace becomes richer in that now each chunk is contributing at an offset. So the acceptnew[psi|lambda|vpsi] methods would all need to paste the input of a contribution at the correct offset. This recalls the old contiguousreducer logic which did that pasting together in its reduction client. A functionality that is arguably worth resurrection. Just in a form that can actually be comprehended by people not from planet brainiac.
Which means we should add a distinct parameter for the number of ortho objects. We'll also need to come up with a way for it to map its grainsize sections onto the chunketized PC chare array. The constraints on this mapping are only that they should use as many PCs as we can. The PCs will use the section reduction in their forward path reduction to deposit the S (or lambda) matrix in ortho. Ortho will have to broadcast its T (or lambda, or orthoT and gamma) to the PairCalculator.
Which returns us to the bad old days of broadcasting matrices around. This can be ameliorated slightly by using [nokeep] messages so that we reduce the number of copies to 1 per PE. But you still have to send numPE*nstates*nstates doubles around (times 2 in the dynamics symmetric case to carry ortho and gamma). Luckily broadcasts turn out to be pretty fast on BG/L. So this may not be so bad. The tradeoff against the much larger nonzero multicast is net positive due to the larger constant size of the nonzeros compared to nstates.
These communication patterns become more complex in the hybrid case where we have both grainsize and chunksize. The ortho->PC section mapping could revert to using grainsize, but now has to sum across all the chunks in that grain.
If we want independant control over the number of ortho objects then we need to support the overlap issues where grainsize objects do not map nicely onto ortho objects.
The reduction out of the backward path of the paircalculator is the one which is made more complicated by 4th dimension decomposition. Here we are sending the transformed Psi, which is necessarily numpoints in size. Therefore the reduction requires stitching of blocks while summing within a block to assemble the entire g-chare matrix of points. In practice this is just one big reduction with the userfield used to indicate the chunk number so gspace can lay the results out where they belong.
In its current form orthoGrainSize must be an even mod of sGrainSize. This restriction avoids overlap and boundary issues for tiles between ortho and the calculator. Thereby avoiding some rather gnarly issues in the setup of multicasts and reductions. This is a fairly minor restriction as long as we do not require nstates % sgrainsize==0 or nstates & orthograinsize.
sGrainSize need not be even mod of the number of states. nstates % sGrainSize = remainder requires some careful handling in the code. Whenever this occurs the multiplies and communications for the border edges which carry the remainder have to cope with asymmetric multiplies and funky remainder logic in communicating the result.
Data from GSP travels to the PairCalculators via an InputDataHandler chare array of the same dimensions as, and bound to, the PairCalculator array. Appropriate sections/lists of this input handler array for multicasting the data from GSP to are built in makeLeftTree() and makeRightTree().
Each iteration of the GSP-PC-Ortho-PC-GSP loop is started by GSP calling startPairCalcLeft() and startPairCalcRight(). These are simply #defines that turn into the appropriate function: sendLeftData() and sendRightData() or their RDMA equivalents. The input handler chares then collate all the incoming data and then wake their corresponding PC chares once all the data is available. The PCs then do their thing and the result is returned via the callback set in the create routine (which happens to be Ortho).
The backward path is triggered by multiplyResult() Its result is returned via the callback entry point passed in during creation
The results of the backward path are returned in a set of section reductions. The reduction contributes its slice of its matrix of doubles with the offset=thisIndex.z. The client then returns the sum of each slice to the GSP element that created the section with the offset so it can be copied into the correct place in the points array.
NOTE: The magic number 2 appears in 2 contexts. Either we have twice as many inputs in the non diagonal elements of the matrix. Or in the case of transforming our arrays of complex into arrays of doubles. This transformation is done so we can use DGEMM instead of ZGEMM. Motivated by the empirical discovery that BLAS implementors do all their work on DGEMM and leave ZGEMM out in the unoptimized cold. The latter issue crops up everywhere we have to do allocation or manipulations of the input. Could arguably be abstracted away by absorbing it into a size field.
After the main::main proc 0 phase the array sections used to populate and return data from the paircalculator are called. The forward path section reduction (to and from ortho) is initialized via initOneRedSect() the backward path is initialized via the appropriate makeOneResultSection_X() call. In each case the call should be made by each GSP or Ortho object. That way each one has its own proxy and the section tree will only include relevant processors.
The chunk decomposition changes the setup substantially. In chunk decomposition we send a piece of the nonzero points of gspace to the paircalculators. It is not a multicast. Each GSP[P,S] will send its ith chunk to PC[P,0,0,i]. Once nstate chunks arrive at a PC the multiply can proceed.
In the hybrid case this becomes a multicast of chunks to the appropriate state decomposition destination as before.
Function Documentation
|
inline |
forward declaration
forward declaration
possibly faster than CkReduction::sum_double due to minimizing copies and calling CmiNetworkProgress
Definition at line 23 of file ckPairCalculator.C.
