

Go to the source code of this file.
Functions | |
| int | METIS_PartGraphRecursive (idx_t *nvtxs, idx_t *ncon, idx_t *xadj, idx_t *adjncy, idx_t *vwgt, idx_t *vsize, idx_t *adjwgt, idx_t *nparts, real_t *tpwgts, real_t *ubvec, idx_t *options, idx_t *objval, idx_t *part) |
| Recursive partitioning routine. | |
| idx_t | MlevelRecursiveBisection (ctrl_t *ctrl, graph_t *graph, idx_t nparts, idx_t *part, real_t *tpwgts, idx_t fpart) |
| idx_t | MultilevelBisect (ctrl_t *ctrl, graph_t *graph, real_t *tpwgts) |
| void | SplitGraphPart (ctrl_t *ctrl, graph_t *graph, graph_t **r_lgraph, graph_t **r_rgraph) |
$Id: pmetis.c 10513 2011-07-07 22:06:03Z karypis $
Definition in file pmetis.c.
| int METIS_PartGraphRecursive | ( | idx_t * | nvtxs, | |
| idx_t * | ncon, | |||
| idx_t * | xadj, | |||
| idx_t * | adjncy, | |||
| idx_t * | vwgt, | |||
| idx_t * | vsize, | |||
| idx_t * | adjwgt, | |||
| idx_t * | nparts, | |||
| real_t * | tpwgts, | |||
| real_t * | ubvec, | |||
| idx_t * | options, | |||
| idx_t * | objval, | |||
| idx_t * | part | |||
| ) |
Recursive partitioning routine.
This function computes a partitioning of a graph based on multilevel recursive bisection. It can be used to partition a graph into k parts. The objective of the partitioning is to minimize the edgecut subject to one or more balancing constraints.
| [in] | nvtxs | is the number of vertices in the graph. |
| [in] | ncon | is the number of balancing constraints. For the standard partitioning problem in which each vertex is either unweighted or has a single weight, ncon should be 1. |
| [in] | xadj | is an array of size nvtxs+1 used to specify the starting positions of the adjacency structure of the vertices in the adjncy array. |
| [in] | adjncy | is an array of size to the sum of the degrees of the graph that stores for each vertex the set of vertices that is adjancent to. |
| [in] | vwgt | is an array of size nvtxs*ncon that stores the weights of the vertices for each constraint. The ncon weights for the ith vertex are stored in the ncon consecutive locations starting at vwgt[i*ncon]. When ncon==1, a NULL value can be passed indicating that all the vertices in the graph have the same weight. |
| [in] | adjwgt | is an array of size equal to adjncy, specifying the weight for each edge (i.e., adjwgt[j] corresponds to the weight of the edge stored in adjncy[j]). A NULL value can be passed indicating that all the edges in the graph have the same weight. |
| [in] | nparts | is the number of desired partitions. |
| [in] | tpwgts | is an array of size nparts*ncon that specifies the desired weight for each part and constraint. The {target partition weight} for the ith part and jth constraint is specified at tpwgts[i*ncon+j] (the numbering of i and j starts from 0). For each constraint, the sum of the tpwgts[] entries must be 1.0 (i.e., ![$ \sum_i tpwgts[i*ncon+j] = 1.0 $](form_0.png) ). A NULL value can be passed indicating that the graph should be equally divided among the parts. ). A NULL value can be passed indicating that the graph should be equally divided among the parts. |
| [in] | ubvec | is an array of size ncon that specifies the allowed load imbalance tolerance for each constraint. For the ith part and jth constraint the allowed weight is the ubvec[j]*tpwgts[i*ncon+j] fraction of the jth's constraint total weight. The load imbalances must be greater than 1.0. A NULL value can be passed indicating that the load imbalance tolerance for each constraint should be 1.001 (for ncon==1) or 1.01 (for ncon>1). |
[out] edgecut stores the cut of the partitioning.
[out] part is an array of size nvtxs used to store the computed partitioning. The partition number for the ith vertex is stored in part[i]. Based on the numflag parameter, the numbering of the parts starts from either 0 or 1.
| METIS_OK | indicates that the function returned normally. | |
| METIS_ERROR_INPUT | indicates an input error. | |
| METIS_ERROR_MEMORY | indicates that it could not allocate the required memory. |
Definition at line 91 of file pmetis.c.
References AllocateWorkSpace(), Change2CNumbering(), Change2FNumbering(), ctrl_t::dbglvl, FreeCtrl(), gk_malloc_cleanup(), gk_malloc_init(), gk_sigtrap(), gk_siguntrap(), InitTimers(), METIS_DBG_TIME, METIS_ERROR_INPUT, METIS_ERROR_MEMORY, METIS_OP_PMETIS, metis_rcode(), MlevelRecursiveBisection(), ctrl_t::numflag, PrintTimers(), SetupCtrl(), SetupGraph(), ctrl_t::TotalTmr, and ctrl_t::tpwgts.
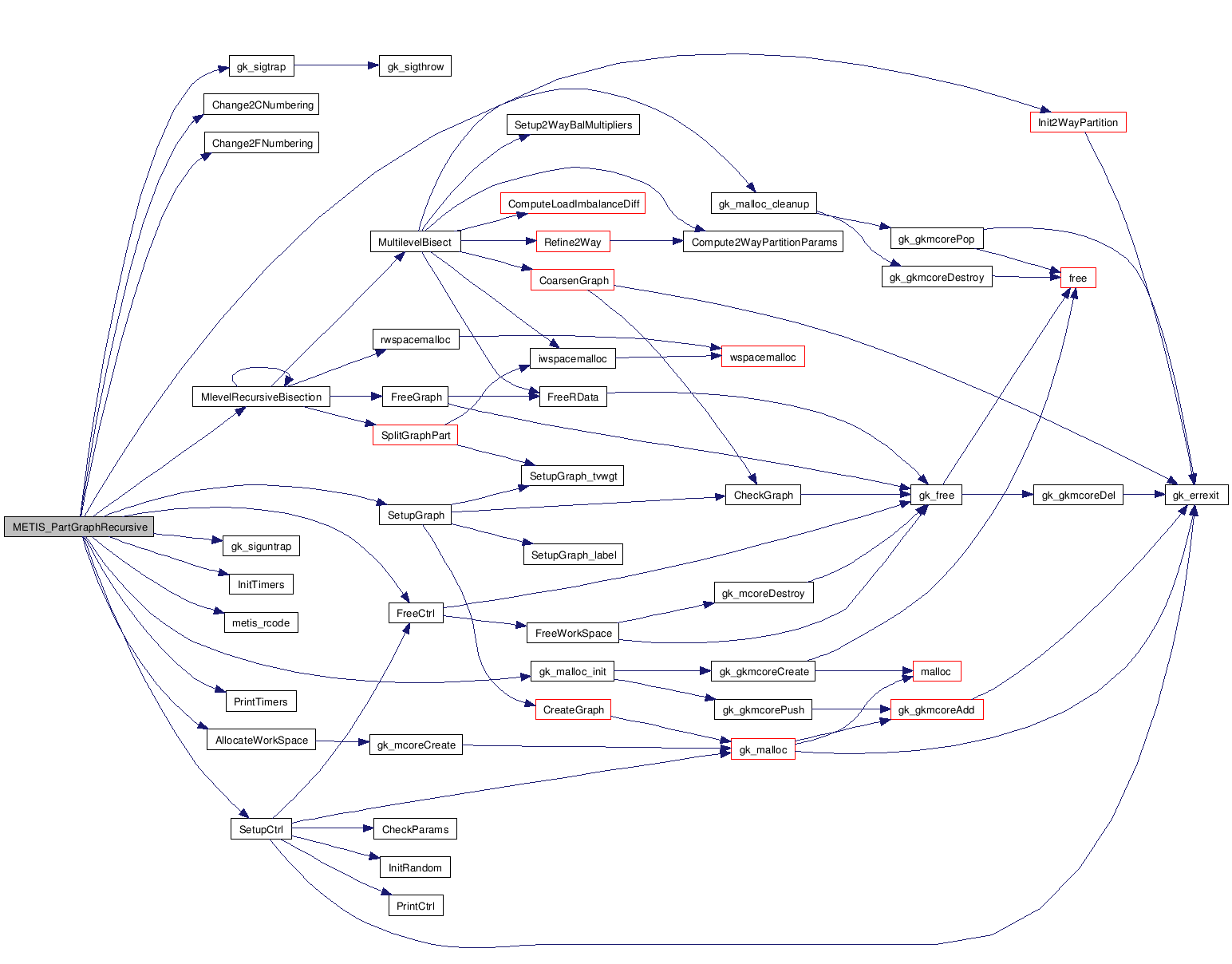
| idx_t MlevelRecursiveBisection | ( | ctrl_t * | ctrl, | |
| graph_t * | graph, | |||
| idx_t | nparts, | |||
| idx_t * | part, | |||
| real_t * | tpwgts, | |||
| idx_t | fpart | |||
| ) |
This function is the top-level driver of the recursive bisection routine.
Definition at line 157 of file pmetis.c.
References FreeGraph(), graph_t::label, MlevelRecursiveBisection(), MultilevelBisect(), graph_t::ncon, ncon, graph_t::nvtxs, objval, rwspacemalloc(), SplitGraphPart(), graph_t::where, and where.
Referenced by METIS_PartGraphRecursive(), and MlevelRecursiveBisection().
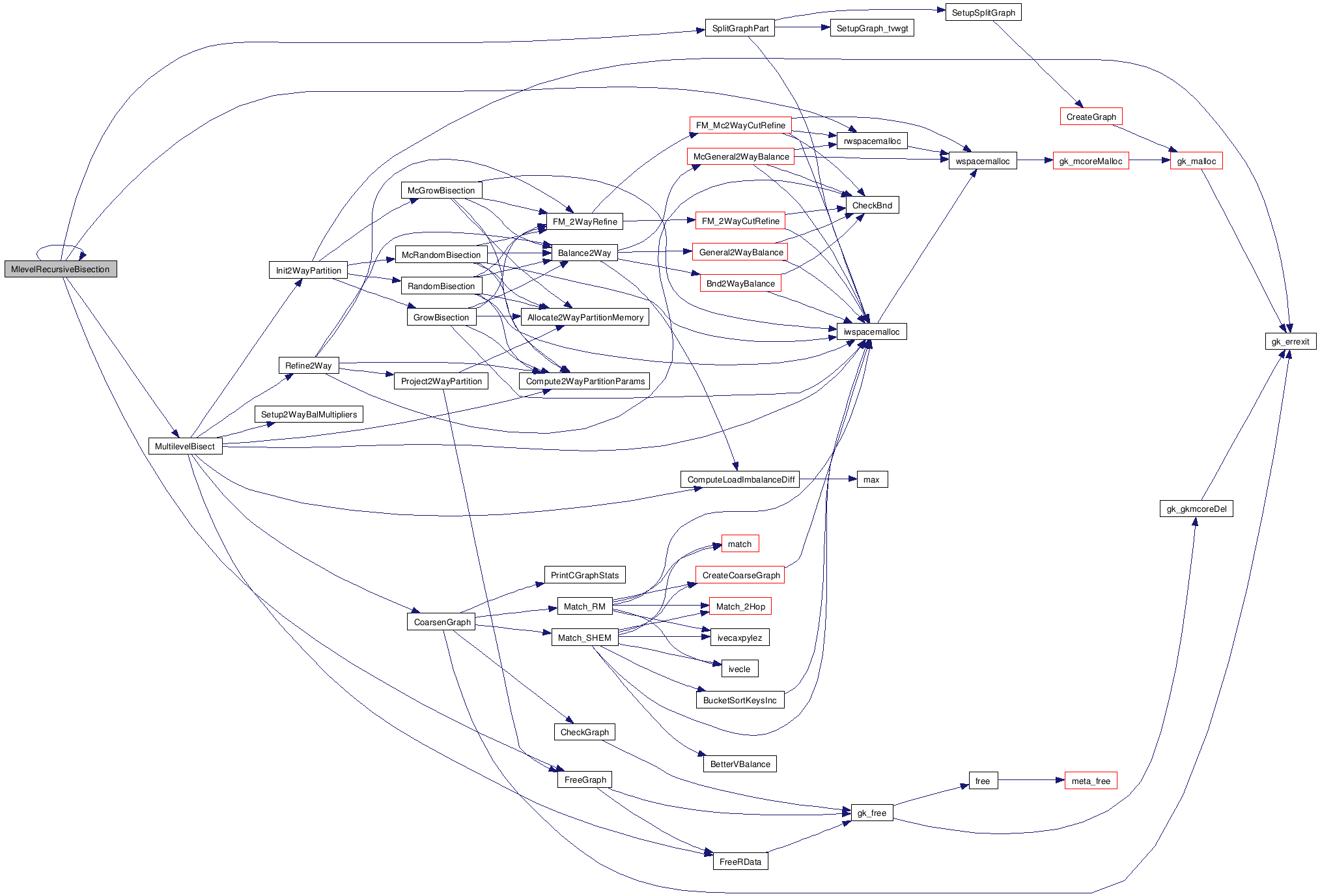

This function performs a multilevel bisection
Definition at line 226 of file pmetis.c.
References CoarsenGraph(), ctrl_t::CoarsenTo, Compute2WayPartitionParams(), ComputeLoadImbalanceDiff(), FreeRData(), Init2WayPartition(), iwspacemalloc(), graph_t::mincut, ctrl_t::ncuts, graph_t::nvtxs, ctrl_t::pijbm, Refine2Way(), Setup2WayBalMultipliers(), ctrl_t::ubfactors, and graph_t::where.
Referenced by MlevelRecursiveBisection().


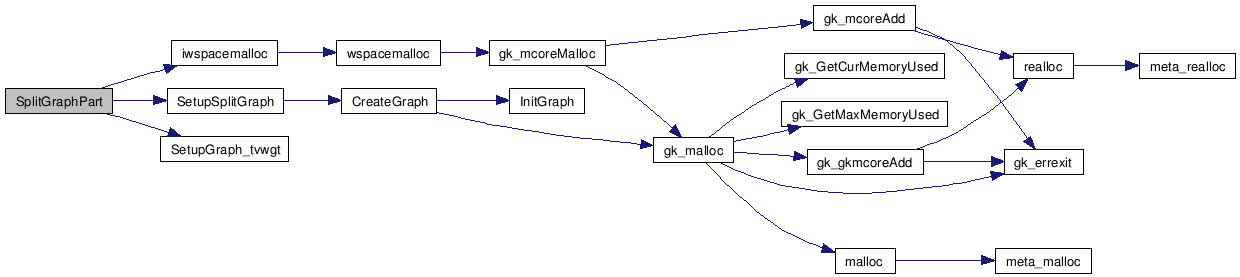
This function splits a graph into two based on its bisection
Definition at line 280 of file pmetis.c.
References graph_t::adjncy, adjncy, graph_t::adjwgt, adjwgt, graph_t::bndptr, ctrl_t::dbglvl, iwspacemalloc(), PUP::l, graph_t::label, METIS_DBG_TIME, graph_t::ncon, ncon, graph_t::nedges, graph_t::nvtxs, SetupGraph_tvwgt(), SetupSplitGraph(), ctrl_t::SplitTmr, graph_t::vwgt, vwgt, graph_t::where, where, graph_t::xadj, and xadj.
Referenced by MlevelRecursiveBisection().

 1.5.5
1.5.5